2次試験はファイナルペーパーを作ろう
branchpine
中小企業診断士 合格ブログ（ぶらんち）
現在価値とは（電卓紹介もあるよ）
branchpine
こんにちは。ぶらんちです。今回はみんな大好き現在価値についてです。
特に事例Ⅳでは頻繁に登場し、しかも相当ややこしいので試験の難易度を上げる要因になっています。
ただ、分かるとライバルとはかなり差がつきますので、気合を入れて取り組みましょう！
スポンサーリンク
現在価値とは
現在価値とは、主に未来のお金（将来価値）を現在の価値に換算したものです。
一般的に、未来のお金よりも現在のお金の方が価値が高いです。
例えば、今手元にある100万円を、金利10%の銀行（…現実にあったらいいなぁ）に預けた場合、1年後には110万円になっています。100万円から労せず10万円の価値を生み出せたということですね。つまり、「今100万円を持っていること」と「1年後に110万円を持っていること」は同じ価値と言えます。この状態を「1年後の110万円の現在価値は100万円である」と表現します。
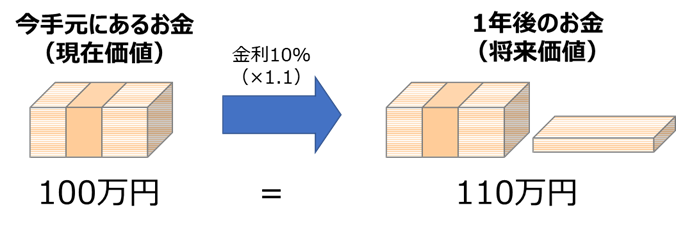
これが現在価値の基本的な考え方です。
では、「1年後の100万円」の現在価値はどうでしょうか？こちらは「100万円÷（1+金利）」で求めることができます。金利が同じく10%の場合は、100万円÷（1+0.1）≒90.9万円です。1年後の100万円と現在手元にある90.9万円は、価値が同じということですね。
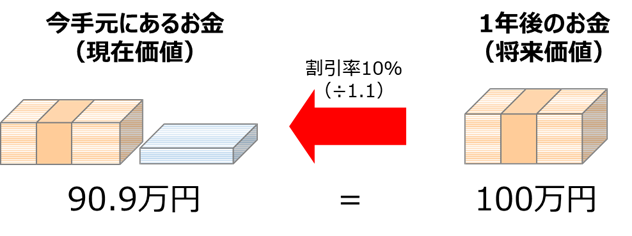
ちなみに、現在価値の計算に使う金利のことを割引率と言います。
現在価値＝将来価値÷（1+割引率）
数年後の現在価値
金利10％の銀行に1年間預け110万円になったお金を、さらに1年間預けた場合、110万円×1.1＝121万円になります。2年目は11万円増えてますね。
さらに1年間預けた場合は、121万円×1.1＝133.1万円となり、3年目は12.1万円増えています。2年目以降は、金利で増えたお金に対しても金利がつくので、どんどん増加幅が大きくなります（これを複利と言います）。
一方、現在価値の観点からみると、2年後の121万円も3年後の133.1百万円も現在価値は同じ100万円ということを表しており、遠い将来ほど価値の目減りが激しいということが分かります。
ちなみに3年後の100万円の現在価値を求めるとこんな感じになります。
現在の75.13万円と3年後の100万円が同じ価値なんて、なんだか不思議ですね～。
複利現価係数
先の計算では、1.1で割ることで現在価値を算出していましたが、（1／1.1）を掛けることでも同じ値を得ることができます。
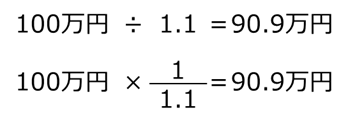
（1／1.1）≒0.909となりますが、この「0.909」のことを複利原価係数といいます。1年後の現在価値などではピンとこないかもしれませんが、10年後、20年後の現在価値を算出するときなど、遠い将来に対して現在価値を算出するときに便利です。いちど複利原価係数を計算しておけば、100万円が200万円になっても（例え132万円と中途半端な金額であっても）即座に現在価値を求めることができます。
1次試験では、複利原価係数を求める問題も出てくることがありますので、基本的なルールとして押さえておきましょう。
年金現価係数
例題
A社では今後5年間、毎年900万円の利益が発生する。5年間の利益の現在価値はいくらか。ただし、割引率は10%とし、複利原価係数は以下表を用いることとする。
単純に計算すると、以下の通りとなります。
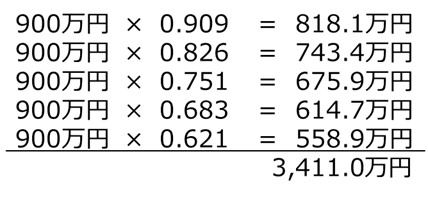
ただ、これでは計算ミスも増えますし、何より時間がかかります。そこで予め複利現価係数を足してしまいます。
複利現価係数を年数分足し合わせたものを年金現価係数と言います。各年の金額が同じ場合は、年金現価係数を使った方が効率的です。本試験では、以下のように表として与えられていることが多いです（以下は割引率10％の場合）。
実践問題
例題
X1期首における現在価値を計算せよ（単位：百万円）。端数処理は最終結果に対し小数点第３位を四捨五入するものとする。なお、割引率は10％とし、以下係数を用いること。
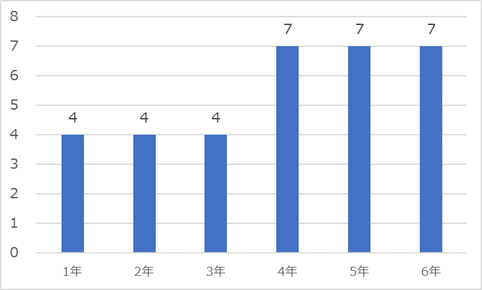
複利現価係数、年金現価係数ともに3年しか与えられていないので、工夫して計算する必要があります。
＜1年～3年目＞
各年全て4（百万円）なので、年金現価係数が使えます。
4×2.478＝9.912（百万円）
＜4年～6年目＞
ここも3年間同じ7（百万円）なので、年金現価係数を使いましょう。
7×2.478＝17.346（百万円）
ただし、上記は3年期末時点の現在価値なので、さらに複利現価係数をかけて1年目期首の現在価値に直します。
17.346×0.751＝13.0268…（百万円）
よって、9.912＋13.0268…＝22．938… ≒22.94（百万円）
おすすめの電卓
特に2次試験では、使いやすい電卓の存在が大きかったりします。ここでは、ぶらんちがオススメする電卓を紹介します。
電卓はシャープ派とカシオ派が激しい派閥争いをしています（ウソです）が、ぶらんちはカシオ派です。
当然ながら2次試験に持ち込める条件を全てクリアしています。
ボタンが大きくて押し間違いが少ないし、メモリ機能はもとより自動で四捨五入してくれる桁切替スイッチやGT（今までの計算を全て合算）などの機能が充実しており、使いこなせばかなりの時間短縮になります。
ただ、ぶらんちの場合は、「複利現価係数」の算出操作を覚えているのがこの電卓だけだった、というのもあります（他の電卓怖くて使えない…）。
複利現価係数の算出方法
※ カシオ電卓（JT-120GT）の場合
- １＋割引率を入力（10％の場合は1.1）
- 「÷」を2回押す（液晶上部に「K」がつく）
- １を入力
- 「＝」を入力すると1年目の複利現価係数
- もう一度「＝」を押すと2年目の複利現価係数
- 以降、知りたい年数分「＝」を押す
※ 年金現価係数が知りたい場合は、上記操作後、最後に「GT」を押す
最近は係数表が明示されていることの方が多く、あまり使わないかもしれませんが、覚えておいて損はないです。
JF-120GTの廉価版です。サイズも一回り小さいです。2次試験には電卓の故障に備え2台持っていくのが常識なのですが、サブ機としてちょうど良いサイズかと思います。
ただ、ぶらんちはJF-120GTを2台購入しました。MN-12GTは液晶の角度が変えられないのが自分的にはマイナスポイントだったってのもありますが、故障のようなトラブルが起こると焦るじゃないですか。そんなときこそ同じ電卓が準備できた方が心が落ち着くんじゃないかな～って思ったからです。
ちなみに、電卓の操作方法を解説してくれる本があったのでご紹介します。試験問題での実用方法なんかも載っており、中小企業診断士試験以外の試験対策でも使えると思います。
まとめ
如何でしたでしょうか。
2次試験の計算ミスは、ほとんどが現在価値の計算の場合が多いです（…と思います）。正しく理論を理解して、使いやすい電卓で本試験に臨みましょう！
ABOUT ME
